Pythagorean Theorem Calculator
Calculate the sides of a right-angled triangle with step-by-step solutions.
※ Use if necessary
Pythagorean Theorem Calculator
Solve for the hypotenuse or sides of a right-angled triangle with detailed step-by-step solutions.
These results are for reference only and were developed for educational and testing purposes. You can also directly access and review the source code, including the logic and free APIs used on this page.
Calculation Results
Pythagorean Theorem Calculator Guide
The Pythagorean Theorem Calculator is a tool designed to calculate the sides of a right-angled triangle with detailed step-by-step solutions. This guide provides instructions for using the calculator and objective information about the Pythagorean theorem.
How to Use the Pythagorean Theorem Calculator
Follow these steps to calculate the sides of a right-angled triangle:
- Enter Known Sides: Input the lengths of side A and side B, or one side and the hypotenuse, depending on what you want to find.
- Specify Calculation: Select whether you want to calculate the hypotenuse (c) or one of the sides (a or b).
- Calculate: Click "Calculate" to view the result and detailed solution steps.
- Review Results: Examine the calculated result, formula used, and step-by-step solution.
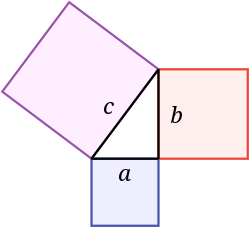
Licensed under GFDL 1.3
About the Pythagorean Theorem
The Pythagorean theorem calculates the length of sides in a right-angled triangle.
Formula
- a, b: Lengths of the two legs (shorter sides)
- c: Length of the hypotenuse (longest side)
- Can calculate any side when the other two are known
- Only applicable to right-angled triangles
Mathematical Concepts
- A triangle with one 90-degree angle
- The side opposite the right angle is the hypotenuse (longest side)
- The other two sides are called legs
- Pythagorean theorem relates the lengths of all three sides
Final Tips for Using the Calculator
- Ensure you enter positive values for known sides.
- When finding a side, provide one side and the hypotenuse, ensuring the hypotenuse is longer.
- Review the step-by-step solution to understand the calculation process.
- For complex problems, consider verifying results with alternative methods.
The calculator provides solutions based on the Pythagorean theorem. For specialized applications, consult additional references.